[Note added on 2-7-14: This is one of my most-read posts. If it helps you design a good project for your class, that's great. Please do not use it as is. Make adjustments for the age of your students (mine are in college), and fill in the details where I've put notes in brackets. Make sure you try each part out yourself before using this with students! To do otherwise is to ask for trouble.]
There've been some great discussions on teaching logarithms recently at
JD2718 and
f(t). At JD's blog, I mentioned a project I do in my classes, and nyates asked for the details. Here it is - just enough hook to get students working pretty well in groups. (One class decided we were CSI at CCC.) :^) But in my opinion, they're still mostly following the formula. If you have any ideas for improving this, I'd love to hear them.
Years ago, I shared my office with a chemistry teacher. When she complained that we math teachers often did a bad job in Intermediate Algebra courses with the (vital to chemistry) topic of logarithms, I decided to try to do it better. It was right at the end of the course, which always means neglect, so I moved it up a bit somehow. I also wanted to pull the students in more, so I made this project up.
This project uses Newton's Law of Cooling, though I don't mention that. (I often get students coming in the second day with that information. They've searched online, and found it. Good and bad - I like the research skill and initiative, but they want to use the formula they've found, instead of reasoning it out.) I work with them to figure out:
body.temp = air.temp + excess.temp.at.time0 * b ^ t, where body.temp is a function of time, air.temp is constant, excess.temp.at.time0 is how much hotter the body was than the air when first measured, b < 1 (exponential decay), and t is measured in hours or minutes. The only log work necessary is:
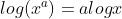
, so this doesn't get them practicing the other log properties.
To help them remember when to use logs, I tell them that historically logs helped people multiply, divide, and find roots, but that now calculators do all that, so
"the purpose of logarithms is to get the variable out of the exponent." (What do you think? Is that problematic?)
I have them get in groups, and give them maybe half an hour each day to work on the assignments. They've worked with exponential functions, and I start this project as we begin working on logarithms.
I play
the theme music from Gilligan's Island to start class on the day we begin, and I tell them...
"Our whole class has gone on a cruise together and been shipwrecked. There's plenty to eat and drink, so no one's too stressed. But then, our classmate John Doe is murdered! (He was so quiet, you may not remember him.)"
Then I give them this:
Shipwreck and Murder
You’ve all been shipwrecked on a tropical island - a wonderful place, with bananas, coconuts, fish, and a pretty constant temperature of 80°. Your classmate, John Doe, has been murdered. You know there’s no one else on the island - it was one of your classmates that did it! None of you will sleep peacefully in your flimsy grass huts until the murderer is discovered.
You have watches, thermometers, and other simple tools, but no experts on murder investigations. The day John was murdered, everyone was walking around the island by two’s, noting its features, in hopes that would help you all figure out where you are. It turns out that everyone walked by the spot where John's body was found, and recorded the time when they were at a nearby spot (where they could see a volcano on the next island). Figuring out the time of death would likely narrow down the suspects to four or less.
Angel had a hunch that knowing the body temperature would help determine the time of death. So, at 1 pm, she checked the temperature of John’s corpse. It was 96.1°. Then at 2 pm, it was 91.7°.
Finding the murderer will be our goal. It might take us a few days. (I hope you don’t mind some sleepless nights...)
One more clue… this comes from Daniel, “I read a lot of murder mysteries. In one of them, this detective says, ‘A dead body cools off just like a hot cup of joe.’ I don’t know if that helps or not…”
~ ~ ~ ~ ~ ~ ~ ~
[Change Angel and Daniel to the names of students in your class.] After they've read this, and asked me questions about fingerprints, how he was killed ("looks like a coconut to the head"), and a few other distractions, I ask them to do the following assignment.
Assignment 1
[Do each of these assignments in groups of 3 or 4. If you want, you can turn in one copy per group. It will be important later to be able to describe how your understanding of the problem changed over time, so each person should keep neat notes on the case.]
We want to think about how a hot cup of coffee cools off.
1. What would be a reasonable starting temperature?
2. After about how long would it be cold?
3. About what temperature is it when it’s cold? (Why?)
4. Now let time be the x-axis (t-axis) and temperature (T) be the y-axis, and (on graph paper) graph temperature versus time for a cop of coffee, using what you know from common sense. Does a straight line graph make sense for this?
~ ~ ~ ~ ~ ~ ~ ~
I get a few volunteers to promise to actually measure the temperature of a cooling cup of hot water, and point out that old fashioned mercury thermometers will break and other body temp thermometers might break - they'll need a lab thermometer or a cooking thermometer. No matter how many people promise to do this, I know I might have no data by the next day, so I've saved data from an old class.
Assignment 2
Sarah says “We need some numbers here.” And she boils some coffee up over a campfire and measures its temperature with a thermometer Jessica provides.
Here’s what she gets:
The coffee starts out at 176 degrees, and cools off like this…
Min Degrees
1 169
2 162
3 156
5 146
10 125
15 111
20 101
30 90
60 81
1. If he measured the coffee at 2 hours and 3 hours, what temperature would it be?
2. Graph this data, and connect the points with a smooth curve.
3. So we can conclude that this graph has what line as an asymptote?
4. Give an example of a function with this asymptote.
~ ~ ~ ~ ~ ~ ~ ~
Assignment 3
John Doe’s dead body was lying near the viewing spot for the volcano, and it turns out that there was only one path going by that spot. So, after checking with each other, and remembering who passed whom, you all agree that the murderer was most likely one of the people at that spot right before or after the time of death.
Below are the times that each pair walked by the volcano viewing spot:
Colleen & Mouang 11:15am
Tiana & Armoriana 11:38
etc... (all class members listed)
Paolo & Vithaya 1:24pm
When you figure out the time of death, you’ll know the 4 most likely suspects.
Time of Death:
Suspects:
[Note: Before typing up this list in assignment 3, I've figured out the time of death, checked with the class to find out whether anyone objects to playing the killer, and made sure no one who'd be uncomfortable with it will be a suspect. The idea is that the time of death will be between two of the times listed, and the 4 people listed for those 2 times are the suspects. To find the time of death, they'll solve the equation body.temp = air.temp + excess.temp.at.time0 * b ^ t for the time that the body was 98.6 degrees, which will be the time of death. If we've let the first temperature measured be at time 0, then the time we get from this equation will be negative. That's a nice switch, since some of them think story problems can never have negative answers.]
[Note added on 2-7-14: If you are a teacher planning to use this, the
idea is to use your own students' names here. Make sure none is walking
by at the exact time of death, so that the pair just before and the
pair just after are both suspect, and have pairs walk by every 5 to 15 minutes.]
~ ~ ~ ~ ~ ~ ~ ~
Assignment 4: The Next Day
Of course, all 4 suspects swear they’re innocent. The next day, Rasha finds
me dead, left lying right in the clearing.
My body temperature is 93.1°, and it’s 9:46am. You check at 10:16am, and it’s 87.2°.
Here’s everyone’s alibis:
• Colleen, Tiana, Robyn, Pardeep, Maureen, Jianfei, and Tayyaba were all swimming together from 8am to 9:30am.
• Brandon, Adeyinka, Cristina, Ash, Cookie, and Paolo were all looking for clams together from 8:30am to 9:30am.
• Mouang, Armoriana, JoAnn, Adam, Denisha, Edith, and Angel were all gathering coconuts together from 9am until they heard Kevin’s screams.
• Daniel, Josue, Natalie, Danielle, Dwight, and Vithaya were hiking from 9:30 until they heard the screams.
Please find the killer before someone else is murdered!
[Note: Students often like to accuse me of being the killer, so I get killed next. I tell them I think it's because I knew too much. The list of names puts each of the 4 suspects in a different group. The one without an alibi is the serial killer.]
I do this project in Intermediate Algebra (the community college equivalent of a high school Algebra II course, done in one semester) and in Pre-Calc. In Pre-Calc, I often end with an assignment to each write up their closing arguments as prosecuting attorney, explaining to the jury how we know the time of death, and why that means the prime suspect is the killer. A lot of them have fun with that assignment.
I give them a problem like this on their next test, and it's not great. I wish I had collected data on success rate on that question. It's probably less than half of the students. Worse than other questions...
[Notes added on 2-7-14:
- Well, I'm not sure when it shifted, but they do better on this test problem these days.
- If you plan to use this, you will need time to fix up the two lists of names. Work the problems out ahead of time, so you know how it will play out in class.]
Please comment, critique, and suggest improvements.





