Carnival of Mathematics

The Math Less Traveled will be hosting the Carnival of Mathematics this coming Friday. Here's the post about it.

The last two were the 51st Carnival of Mathematics, hosted at squareCircleZ and Carnival of Mathematics #52, hosted at The Number warrior.


Seen any good math lately?

Tests .... (TIMSS & the MA teacher licensing test)

Part I. TIMSS.

Lately I've been reading a lot about the Trends in International Mathematics and Science Study, which has helped us compare the performance of U.S. students in math to that of students in other countries. It was given to students in 4th and 8th grades in 1995, 1999, 2003, and 2007, and the U.S. performs well below a number of countries, including Japan. Until just now I hadn't really thought to question the validity of the study.

But when I went to the NCES (National Center for Education Statistics) website, I saw Dare to Compare, where you can test yourself on the questions kids get. The very first question (I said I wanted 12th greade level) was on statistics, and required knowing the factoid that about 95% of all values in a normal distribution lie within two standard deviations of the mean. That's an arbitrary sort of thing, and not representative of important mathematical skills, in my opinion. [Added:] About 1/4 of the questions seem to be about probability and statistics.

Here's the question:

1. A clock manufacturer has found that the amount of time their clocks gain or lose per week is normally distributed with a mean of 0 minutes and a standard deviation of 0.5 minute, as shown above. In a random sample of 1,500 of their clocks, which of the following is closest to the expected number of clocks that would gain or lose more than 1 minute per week?

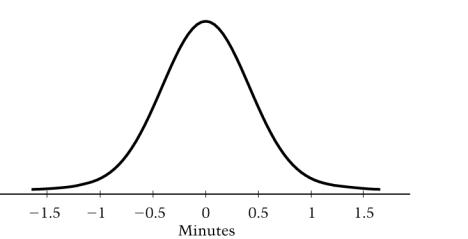The answers provided are 15, 30, 50, 70, and 90. Before teaching statistics, I'd have estimated the area in the tails by sight, and guessed something less than 10% (150), and picked 90, which is wrong.

One bad question isn't enough to invalidate a whole test, but it does make me question the judgment of the people who created it. (Of course, it could be that the website questions aren't as carefully screened as the real test questions...) [Added:] Of course, if all 12th graders are expected to have taken statistics, then there's not much problem. Is that the case these days?


Part II. MA Teacher Licensing Test

Massachusetts recently instituted a math test required for teachers to get licensed. Only 27% of the people taking this test passed it. [The score needed to pass is not available, as far as I can see.] Are the candidates unprepared mathematically? Most likely some of them are. Is the test reasonable? Well, you can get it here, and judge for yourself. [Note: A news article originally led me to the wrong test, what looks like a math subject test for the high school teachers. Thanks, Colleen for pointing out the right one. Both are on this page.]

The test has 45 multiple choice questions and an essay question, in which the test-taker is asked to evaluate a student's work. I took the test just now, and got a few wrong. (Achoo! My brain doesn't work today, with this cold.) About 2/3 of the questions should be pretty straightforward for someone well-prepared. Then there's 12 to 15 questions that will really take some thinking. Is that too much to ask in the stressful situation of a licensing test?

[Commentary on wrong test deleted.]

Here's a quote from a Boston Globe article:

"The failure rate isn't because we have placed some arcane, really hard, high-level math on the test," said Robert Bickerton, associate commissioner for the Elementary and Secondary Education Department, "What we've done is say you need to know this math deeply and you need to be able to answer your students when they ask why."

Hmm, I wonder if he's taken the test. I do want math teachers to be able to think deeply, but this test may be asking a lot. I guess I'd make it a bit shorter, and maybe put the more straightforward questions first. What do you think?

[Burt pointed out some great articles, but his links didn't work. I don't know how to do links in comments, so I'm adding them here: Patricia Kenschaft at 2005 AMS meeting, Racial Equity Requires Teaching Elementary School Teachers More Mathematics, and Deborah Ball et al, Knowing Mathematics for Teaching]

Math Teachers at Play #8

Math Teachers at Play #8 is up at Let's Play Math. Thanks, Denise, for gathering so much good material together! Looks like I'll be exploring it for the next few days.

Math, Crochet, Coral Reefs, Global Warming, Oh My!

I was following a reference in the book What's Math Got to Do with It? (Jo Boaler), in which she quoted Margaret Wertheim as saying she was enchanted by pi. I loved the quote and thought I should read it in its original source.

I googled and found The Institute for Figuring, whose photo gallery shows hyperbolic geometry illustrated through crocheted pieces. Why might you care about hyperbolic geometry, if you're not particularly into math? (from the press page:)

For Ms. Wertheim ... the project embodies the “beauty and creativity that comes out of scientific thinking,” what she refers to as “conceptual enchantment.” As it turns out, the gorgeously crenellated, warped and undulating corals, anemones, kelps, sponges, nudibranchs, flatworms and slugs that live in the reef have what are known as hyperbolic geometric structures: shapes that mathematicians, until recently, thought did not exist outside of the human imagination.

... the Hyperbolic Crochet Coral Reef is much more than a warning about global warming. It marks the intersection of the Wertheims’ [Margaret's and her twin sister, Christine's] various passions: science, mathematics, art, feminism, handicrafts and social activism.

Now those are some renaissance women! They know that it's all connected, and Margaret is moved by 'conceptual enchantment'. I'd like to meet her some day!

(Back to looking for the quote that got me started...)

Improving Education (twitter-style)

tweet

(An experiment in Twitter-like communication in a more permanent medium, which Maria Droujkova pointed to at her blog, Natural Math.)

Math Student's Bill of Rights, by Sandra L. Davis

I have the right to:


Learn at my own pace and not feel stupid if I'm slower than others,

Ask whatever questions I have,

Need extra help,

Ask my teacher for help,

Say I don't understand,

Not understand,

Feel good about myself regardless of my math abilities,

Not base my self-worth on my math skills,

View myself as capable of learning math,

Evaluate my math teachers and how they teach,

Relax,

Be treated as a competent adult,

Dislike math,

Define success in my own terms.

Adapted from the Math Anxiety Bill of Rights by Sandra Davis, in Resource Manual for Counselors/Math Instructors: Math Anxiety, Math Avoidance, Reentry Mathematics, ed. by Donaday & Auslander (1980).

I put this into my syllabus for all my lower level classes. I also have it on my office wall.

I tell students that schools aren't always the best way to learn math, because they can make it pretty hard to learn at your own pace, if the course is paced faster than you need to learn it.

Teaching Undergraduate Mathematics...

... another conference at MSRI. I didn't ever manage to adequately describe the Great Circles conference held there last month. Don't know if I can do any better with this one.

I missed the morning sessions, because I was teaching. It's our last week of classes at my college, and I wasn't going to cancel too much. The first afternoon session was Maria Terrell talking about the Good Questions Project at Cornell. They asked all instructors of their basic Calc I course to participate, and provided them daily questions to ask, which were broken into 3 groups: Quick Checks, Probing, and Deep. Instructors had the freedom to use what they wanted of the projects' materials.

After the Fall 2003 semester was over, the instructors seemed to fall into 4 groups. The ones who mainly asked the deep questions and used peer discussion with the questions, those who used the questions heavily and included peer discussion, those who used the questions heavily but didn't use peer discussion, and those who didn't participate much. The two groups that used the peer discussion did much better on the common finals. The ones who used the questions heavily but didn't use peer discussion did worse than the ones who didn't participate much.

There was a break, and then there was a shared talk where each presenter got 15 minutes. Jerry Eptstein talked about how our students learn next to nothing from hearing us talk. He talked about a project to get them more engaged. There's a lot of research on good ways to teach physics, and something called a force concepts inventory has seemed to have excellent results. (See Mazur here.) So he's been working on a Calculus Concepts Inventory. He's also worked on something called the Integrated Lab Program, which he thinks can make huge differences. I think he's got some good ideas, but his talk wasn't as well-organized as Maria's.

Tomorrow there will be a talk on the Algebra Project. I'm excited about that.

Math Teachers at Play #6 and Numbers

Math Teachers at Play #6 is up! Over at I Want to Teach Forever.

And here's a conversation I had with my son (6yo) a few minutes ago, right after he woke up:

Me: I'm up to 500 (hits on my blog). I guess now I'll be waiting for 1000.
He: What's a thousand?
Me: (Huh? How do I answer that?) Umm, it's ten hundreds.
He: That's 500 more.
Me: Yep.
He: Ten is just like a hundred, except a hundred is ten times bigger.
Me: (Big grin.)

I love it! And he's no more brilliant than all the other kids who haven't yet been shut down by schooling.

So, I'm thinking my blog hits are growing exponentially. Maybe after I hit a thousand, I could make a chart. Eventually it'll flatten out and be logistic, huh? Anyone else watching how their numbers grow?

The Konigsberg Bridges and 'Borrowing'

I'm planning to play with this problem together with some students today, and with my math salon tomorrow. Before starting to think about that, I was doing my usual early morning wandering through the blogosphere, and most amazingly landed on a post about this very same problem at 360. I'll get to 'borrow' the work Xi did putting together that post.

I'll also be 'borrowing' some great ideas I heard over 20 years ago in a math talk given by John H. Hodges. (I think it was at the NCTM conference in '81 or '82, and I think he was at UC Denver.) He used the Bridges problem to illustrate the steps he laid out in his 5 Major Steps in Mathematical Creation. I'd love to contact him to get his permission to post his notes (I have them on ditto!) here, but so far I haven't managed to find him.

Anyone have any favorite materials on this you'd like to point me to? I wouldn't mind borrowing a bit more... ;>