Tests .... (TIMSS & the MA teacher licensing test)

Part I. TIMSS.

Lately I've been reading a lot about the Trends in International Mathematics and Science Study, which has helped us compare the performance of U.S. students in math to that of students in other countries. It was given to students in 4th and 8th grades in 1995, 1999, 2003, and 2007, and the U.S. performs well below a number of countries, including Japan. Until just now I hadn't really thought to question the validity of the study.

But when I went to the NCES (National Center for Education Statistics) website, I saw Dare to Compare, where you can test yourself on the questions kids get. The very first question (I said I wanted 12th greade level) was on statistics, and required knowing the factoid that about 95% of all values in a normal distribution lie within two standard deviations of the mean. That's an arbitrary sort of thing, and not representative of important mathematical skills, in my opinion. [Added:] About 1/4 of the questions seem to be about probability and statistics.

Here's the question:

1. A clock manufacturer has found that the amount of time their clocks gain or lose per week is normally distributed with a mean of 0 minutes and a standard deviation of 0.5 minute, as shown above. In a random sample of 1,500 of their clocks, which of the following is closest to the expected number of clocks that would gain or lose more than 1 minute per week?

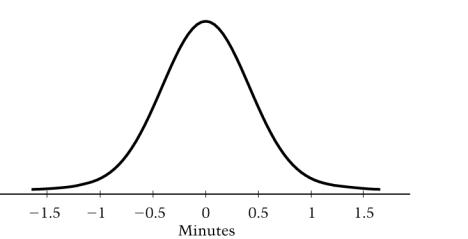The answers provided are 15, 30, 50, 70, and 90. Before teaching statistics, I'd have estimated the area in the tails by sight, and guessed something less than 10% (150), and picked 90, which is wrong.

One bad question isn't enough to invalidate a whole test, but it does make me question the judgment of the people who created it. (Of course, it could be that the website questions aren't as carefully screened as the real test questions...) [Added:] Of course, if all 12th graders are expected to have taken statistics, then there's not much problem. Is that the case these days?


Part II. MA Teacher Licensing Test

Massachusetts recently instituted a math test required for teachers to get licensed. Only 27% of the people taking this test passed it. [The score needed to pass is not available, as far as I can see.] Are the candidates unprepared mathematically? Most likely some of them are. Is the test reasonable? Well, you can get it here, and judge for yourself. [Note: A news article originally led me to the wrong test, what looks like a math subject test for the high school teachers. Thanks, Colleen for pointing out the right one. Both are on this page.]

The test has 45 multiple choice questions and an essay question, in which the test-taker is asked to evaluate a student's work. I took the test just now, and got a few wrong. (Achoo! My brain doesn't work today, with this cold.) About 2/3 of the questions should be pretty straightforward for someone well-prepared. Then there's 12 to 15 questions that will really take some thinking. Is that too much to ask in the stressful situation of a licensing test?

[Commentary on wrong test deleted.]

Here's a quote from a Boston Globe article:

"The failure rate isn't because we have placed some arcane, really hard, high-level math on the test," said Robert Bickerton, associate commissioner for the Elementary and Secondary Education Department, "What we've done is say you need to know this math deeply and you need to be able to answer your students when they ask why."

Hmm, I wonder if he's taken the test. I do want math teachers to be able to think deeply, but this test may be asking a lot. I guess I'd make it a bit shorter, and maybe put the more straightforward questions first. What do you think?

[Burt pointed out some great articles, but his links didn't work. I don't know how to do links in comments, so I'm adding them here: Patricia Kenschaft at 2005 AMS meeting, Racial Equity Requires Teaching Elementary School Teachers More Mathematics, and Deborah Ball et al, Knowing Mathematics for Teaching]