On facebook, I'm in a group for people who use Beast Academy (even though I'm not using it), because Beast Academy fascinates me. I love most of what they do.
A parent today posted that she was confused about the BA way of multiplying 59*59. They have you draw a 60 by 60 box, and then take off one row (of 60) and one column (which is now 59). Your box is now 59 by 59, and its area is 60*60 - 60 - 59. Cool.
She wasn't seeing it, so she taught her kid the standard algorithm. Lots of people were giving her flak for that. (We each do our best, so I don't see why folks would jump on her.) She replied to them that she thought learning it multiple ways was a good thing.
I wrote: "Sure
it's great to do things multiple ways, but does he really understand
the algorithm you showed him? (Do you really understand why it works?) I
think that's why you're getting pushback here."
She said they both understood it. I replied that I'd have trouble explaining to a young kid why you "put a 0". She wrote: "I
just told him we put it to show that the one number is done. I don’t
know if it’s accurate but he understood it. I don’t really remember it
ever being explained in school."
So what she originally meant when she said he understood it, was that he could follow the steps and get it right. Not that he understood why it worked.
I think this is common with math. People think 'understand' means the same as 'can follow the steps'. But I'm afraid that doing math without really seeing why each step makes sense is part of why a lot of people don't like math. It's surely why we easily forget how to do those things.
Here's an article by Richard Skemp, written back in 1978, about why the deeper understanding, which he calls "relational understanding" is a better way to approach math. (He calls being able to follow the steps "instrumental understanding".) I wrote about this topic and this article ten years ago here, but people's ideas about math haven't changed much in that time.
Of course, this parent can still explain to her son why the standard algorithm works, so she hasn't somehow wrecked the beauty of Beast Academy, as some people seemed to feel. And that's what got me writing - I want to see how well I can explain the standard algorithm.
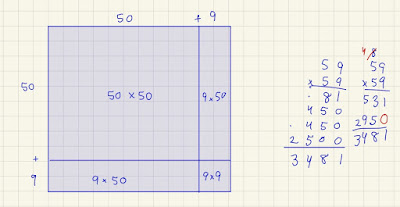
I figure that the standard algorithm packs in a lot with as little writing as possible. (Maybe when we didn't have calculators, and had to do lots of by-hand multiplication, writing as little as possible was considered an important goal for the way we write things down?) So I figured that it needs to be unpacked a little. That's what I tried to do here.
The first calculation is adding up all 4 areas. The one to the far right is the standard algorithm. The first number in the standard algorithm (531) is the 81 and the first 450 added together (with carrying), and the second number (2950) is the other 450 and the 2500 added together. It's surely as little writing as possible, but it hides so much! Does my unpacking on the left help?
It all makes sense to me, but the Beast way feels more fun. (And I don't have to write anything that way. I can hold it all in my head!) What do you think?





As you said, one thing Beast Academy is trying to do is to give students a way to do math in their heads. And even more, they want to lay a foundation for students to understand the formula for factoring the difference of two squares.
ReplyDeleteFor parents, it's so hard to break out of the mindset we picked up in school. We learned that math is about getting answers quickly and efficiently and with as little thought as possible. If you're really good at math, you just look at the problem and know the answer right away, as if by magic.
We weren't taught that not-knowing is perfectly fine, and that the struggle of figuring out how and why something works will pay dividends for years of future learning.
I push on my students to explain the "why" whenever we work with an algorithm. With their help, I will often color code multiple algorithms showing the same problem. Once they see where the numbers are coming from, we push harder to explain why each algorithm works. Some, like the area model Sue showed, are very concrete. Usually when we do the traditional U.S. algorithm (the one on Sue's right) they explain that the zero shows that we are now multiplying 5 tens, not 5 ones so the product doesn't have any ones, it is 295 tens.
ReplyDeleteThanks for commenting, Michelle. I've been inundated by spam comments lately, so it's really nice to get a real one!
ReplyDeleteWhat grade level are you working with?